Class 9 Physics Floatation Notes

In this article, you will get Class 9 Physics Floatation Notes. These are very important from the examination point of view.

Fluids

The substances that flow under the effect of external force are called fluids. These include all gases and all liquids.

Whenever, any force is applied on any gas or liquid, they have a tendency to move. For example, water flows from mountains to plains under the effect of gravitational force.

Pressure

Pressure is the defined as the normal force acting per unit area. The normal force is also known as thrust. Therefore, we can also define the pressure as the “thrust acting per unit area”.

\[\therefore P = \frac{F}{A}\]

Where \(P\) = Pressure, \(F\) = Thrust or normal force and \(A\) = Area on which the force acts.

Density

Density of a substance is defined as the mass per unit volume of the substance. It is denoted by \(D\) or \(\rho\).

So we can say that \(Density = \frac{\text{Mass}}{\text{Volume}}\)

1. If the density of a substance is more, it means the particles are crowded together, and if it is less, it means the particles are far away from each other.
2. The SI unit of density is kg/m³.
3. In general, the density of solids is more than the density of liquids, which is in turn more than the density of gases. That is \(\rho_{solids} > \rho_{liquids} > \rho_{gases}\).
4. Density of a substance plays a huge role in determining whether it will sink, float or rise, when placed in any fluid.

Pressure Exerted by a Liquid Column

Consider a liquid of density \(\rho\) placed in a cylindrical container up to a height h as shown in the figure below.

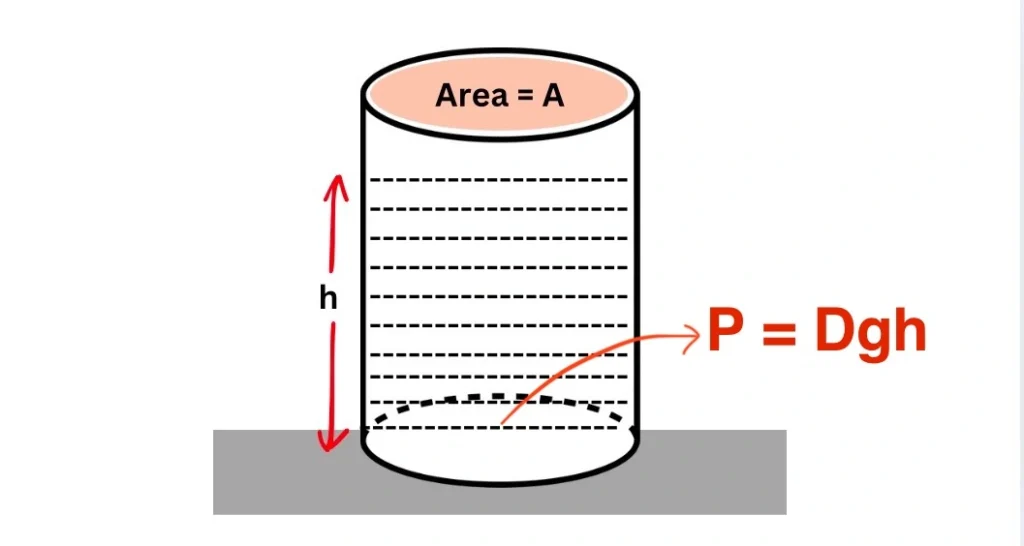
Now let’s find the pressure exerted by the fluid on the bottom of the container.

The force exerted by the fluid column of height h on the bottom is equal to the weight of the liquid column. That is \(F=W\), where \(W\) = weight of the liquid column.

\[\text{Or }F= mg,\] Where \(m\) = mass of the liquid column and \(g\) = acceleration due to gravity.

\[\text{Now using } m=\rho \cdot{V}, \text{we get }\]

\[F= \rho \cdot{V}\cdot{g}\]

\[\text{Or }F= \rho \cdot{Ah}\cdot{g},\tag{1}\] Where \(V = Ah\) is the volume of the liquid column.

Now We know that \(P = \frac{F}{A}\tag{2}\)

Using (1) in (2), we can write

Now We know that \[P = \frac{\rho \cdot{Ah}\cdot{g}}{A}\]

\[\implies P = \rho \cdot{h}\cdot{g}\]

From the above equation, we conclude that;

1. Pressure exerted by a liquid column of height h on any surface is independent of the area of the surface.
2. Pressure exerted by a liquid column is independent of the shape of the container.

Archimedes’ Principle

Archimedes’ principle is an important principle that gives us information about the magnitude of an up thrust experienced by any body when it is placed in any fluid.

According to Archimedes’ principle, “whenever any object is immersed partially or completely in any fluid, it experiences an upward force called Buoyant force or thrust, which is equal to the weight of the fluid displaced by the object”.

Let’s assume that an object of density \(D_o\) is immersed partially or fully in a fluid of density \(D_f\), such that the volume \(V_o\) of the object is in the fluid and \(g\) is the acceleration due to gravity, then the up-thrust (or upward force or bouyant force) experienced by the object is given by;

\[F_u = D_f V_o g\]

Important Points;

1. Upward force experienced by the object is independent of the volume of the fluid in which an object is placed.
2. Upward force experienced by the object is independent of the shape of an object.

Object Placed in a Fluid

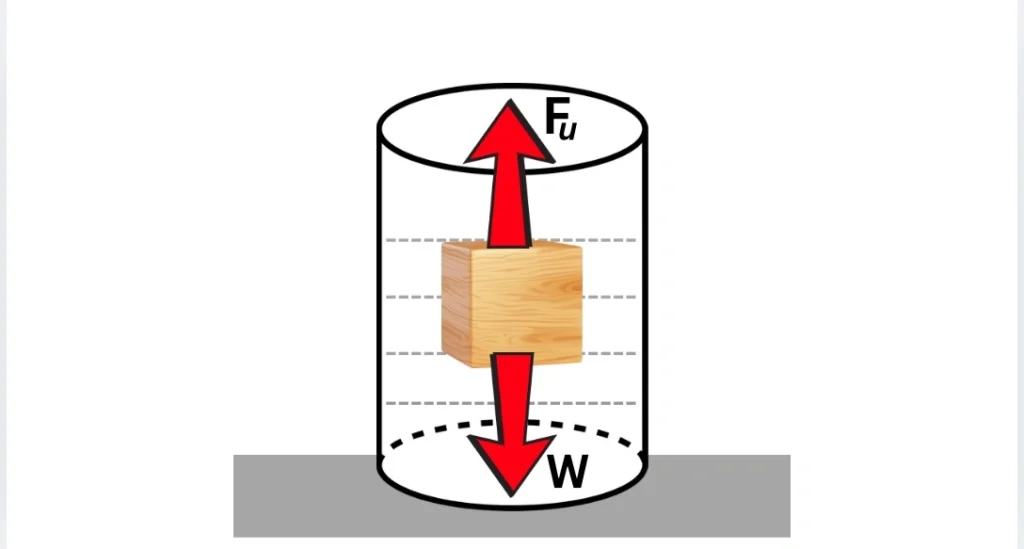
When an object is placed in a fluid, two forces act on it. They are;

1. weight (\( W_o = mg\)), acting downwards.
2. Upthrust (\(F_u = D_f V_o g\)), acting upwards.

Different Cases arise depending upon the magnitude of these two forces (Remember that a body moves in the direction of the net force).

Case 1: When Weight of an object is more than the up thrust.

In this case, downwards force is more than the upward force. The net force acts downwards and hence the object moves downwards and sinks.

Case 2: When Weight of an object is less than the up thrust.

In this case, downwards force is less than the upward force. The net force acts upwards and hence the object moves upwards and floats.

Case 3: When Weight of an object is equal to the up thrust.

In this case, downwards force is equal to the upward force. The two forces cancel each other, and net force is zero. Therefore the body does not move. It floats inside the liquid.

Laws of Floatation

There are three laws of floatation corresponding to the above three cases. These laws are further discussed below.

Law 1: When density of an object \(D_o\) is greater than the density of the fluid, it sinks in that fluid.

Reason: We know that When Weight of an object \(W_o\) is more than the up thrust, it sinks.

It means that for a body to sink;

\[W_o > F_u\]

\[\implies D_o V_o g > D_f V_o g\]

\[\implies D_o > D_f\]

Law 2: When density of an object \(D_o\) is lesser than the density of the fluid, it floats on the surface of the fluid.

Reason: We know that When Weight of an object \(W_o\) is lesser than the up thrust, it rises upwards and floats on the surface.

It means that for a body to float on the surface of a fluid;

\[W_o < F_u,\]

\[\implies D_o V_o g < D_f V_o g\]

\[\implies D_o < D_f \]

Law 3: When density of an object \(D_o\) is equal to the density of the fluid, it floats inside the fluid.

Reason: We know that When Weight of an object \(W_o\) is equal to the up thrust, it is a case of no net force acting on the object. The object floats inside the liquid.

It means that for a body to float inside the fluid;

\[W_o = F_u\]

\[\implies D_o V_o g = D_f V_o g\]

\[\implies D_o = D_f \]

Relative Density (D_R)

Relative density gives us an idea of how dense a substance is relative to water at \(4^0C\).

It is defined as the ratio of density of a body to the density of water at \(4^0C\), and it is denoted bt \(D_R\).

\[D_R = \frac{\text{Density of a body}}{\text{Density of water at \(4^0C\)}}\]

Important Points.

1. Relative density has no units as it is the ratio of similar quantities,
2. If \(D_R >1\), it means the body will sink in water, and,
3. If \(D_R <1\), it means the body will float in water